omdec.com

By Murray Wiseman
Optimal Maintenance Decisions Inc.

Introduction

We should compare the cost effectiveness of an existing maintenance policy with that of a proposed new one, in order to project the benefits of proceeding with that proposed policy. By a policy in CBM we mean, how we will define and declare a potential failure[1]. Setting the threshold (for declaring a potential failure) too low (too conservatively) causes a greater number of premature replacements driving our long-run PM costs unnecessarily high. If the MTTR (mean-time-to-repair) is significant, it will also cause our long-run equipment availability to be very low.

On the other hand, if we set our alert level too high (too liberally) we will experience a larger number of failures than necessary and incur unnecessary costs (and possibly health, safety, and operational consequences) and excessive downtime. We aim, therefore, to set our potential failure declaration (data interpretation) policy at the optimal (best) compromise between the two poles.

The EXAKT[2] methodology is a form of age exploration[3]or reliability analysis. It models (determines the relationship among) the occurrence of failure, preventive renewal, the component’s working age, and relevant condition monitoring (CM) data[4] preceding life ending events. The model, to be used for CBM decision making, must also account for the failure’s economic consequences. Once built and verified, we may use the model as an optimal policy for declaring potential failures. The effectiveness of a proposed policy may be compared with that of current practices by using EXAKT’s “cost comparison” function.

What does CBM Effectiveness depend on?

CBM effectiveness is related, ultimately, to how “good” the condition monitoring data is. That is, how well it reflects the degradation process that takes place internally in the item (and/or how well it measures the accumulated externally imposed stress on the item). In the case of complex items[5], the CM data will be related, in particular ways, to each significant failure mode.

CBM effectiveness is also, quite obviously, highly related to the ratio of the average cost of preventive actions to the average cost of the consequences of failure. Where the consequences of failure are safety, environmental, or health related, then we must measure the effectiveness of CBM in terms of the reduction in the risks related to the failure. Lastly, CBM effectiveness depends, as well, on the quality of data collection, processing, and analysis.

The EXAKT manual explains CBM effectiveness, (for non-safety related consequences), as follows:

When some policy (of PM[6]) is applied, the cost is defined as the average realized cost, i.e. as the ratio of the total realized cost for all lifetimes ending in failure and preventive replacements, and the total realized time for failed and preventively replaced histories. The formula is:

Equation 1

Where C is the cost of a proactive renewal and K is the incremental cost of the failure and its economic consequences (e.g. secondary damage, fines, lost sales, and so on.)[7]

CBM Cost Effectiveness Comparison

In order to assess CBM effectiveness we can consider the costs of three alternative decision (data interpretation) policies:

1. Current policy: The actual rework/discards and failures resulting from existing practice as determined from the sample[8] of historical data
2. Optimal policy: The rework/discards and failures that would have resulted had an optimal decision policy been used to assess (and decide upon) each and every one of the condition data in the sample. There are three ways of calculating the results of the optimal policy to help predict its future effectiveness:

a. Applied: The cost of the policy obtained from applying the optimal model retroactively to the sample.
b. Fitted: The curve of the EXAKT decision chart is fitted to the actual data; so as to minimize “average” realized cost.

i. Fitted, Method A: Suspensions[9] considered as preventive renewals.
ii. Fitted Method B: Suspensions not counted.[10]

c. Theoretical: The warning level boundary curve is selected to minimize “expected” cost.[11]

2. No scheduled maintenance (NSM) policy: The policy of not using any proactive (neither time-based nor on-condition) maintenance.

Rather than describing, in rigorous detail, the calculation methods (especially those of 2.a., 2.b., and 2.c.), as an example, we will assess the effectiveness of a proposed CBM policy. The following data is derived from a study of transmissions in a fleet of mining (300 Ton) haul trucks.

Example of CBM Effectiveness Comparison

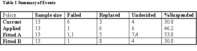
In Row 1 “Current” of Table 1 we note that of the 13 actual life cycles comprising the sample, 6 failed, 3 were replaced, and 4 are “undecided” – i.e. we do not know whether they will eventually fail or be replaced preventively, because, at the time of this “snapshot”, they were still operating.

We may think of a model in CBM as a “measuring stick” for interpreting a set of condition monitoring (CM) data. By using the model, we hope to declare a potential failure, at the “right” time, so that a required long term objective is met. We set our objectives within the model that we build. Those objectives may include: minimal maintenance cost, maximum uptime, some reliability goal, some performance metric, or a compromise among two or more of these.

We build a predictive CBM model by analyzing past equipment failure behavior and coincident CM data. We include, in our model, the economic factors C and K. (C and K were defined in Equation 1 above.)

Row 2 (“Applied”) of Table 1 shows what would have happened had we been able to use the proposed model to interpret actual past CM data. By applying the optimized interpretation model retroactively in this way, we note that 1 transmission still would have failed, 6 would have been replaced and 6 are classified as “undecided”. That is, since these units would have still been in operation at the end of the sample window (no further CM data available), we don’t know whether the model would have predicted, and thus avoided, failure.

The numbers of Table 1 of look promising given that 5 out of 6 failures would have been prevented. However, our assessment, to be fair, must include a judgment of how much of the total operational time and cost we would have “exchanged” for such a decrease in failure rate. We could have been too cautious, preventively intervening too soon (premature replacements) and, therefore, resulting in an expensive PM policy. Our evaluation, however, expands in Table 2.

Procedure for interpreting Table 1 and Table 2

First we examine Table 1. If the number of failed histories of the Current policy (row 1) is significantly reduced by the optimal policy (rows 2, 3, and 4), then we may conclude that applying the optimal policy will significantly influence day-to-day decisions. However, it may or may not produce a true cost reduction. Summarizing Table 1:

· the total number of histories (sample size) is 13,
· with the current policy

o 6 items failed,
o 3 were preventively replaced, and
o 4 are still in operation.

When the proposed optimal policy was applied retroactively to the data set,
· 1 item would have failed,
· 6 would have been preventively replaced, and
· 6 are undecided[15].

From this we conclude that the number of failures would have been significantly reduced. The C+K to C cost ratio used in the optimization model was 6000:1000.[16]

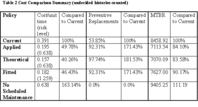
In Table 2 we compare the cost per operating hour of the Current policy with that of the optimal Applied policy to see whether there is any significant reduction in total maintenance costs[17]. This should be the main criterion[18] for acceptance and introduction of a proposed CBM decision policy. From Table 2 the current policy cost is $0.391/h, and the optimal policy cost is $0.195/h. This reduction in (per unit of working age) cost, of about 50%, is significant.

We may also compare the MTBR for both policies. If there is a significant reduction in MTBR (mean time between repairs, either preventive or as the result of failure), the optimal policy is being cautious in reducing failures (due to high cost ratio). If the MTBRs are similar, then the analysis is telling us that our condition indicating measurements (interpreted by the model) are a good predictor of on-coming failures.

In the example, the current policy cost is $0.391/h, and the optimal policy cost $0.195/h. Reduction in cost is about 50%[19]. The percent of preventive replacements for the Current policy is 53.85%[20], and for the Applied optimal policy, 92.31%[21]. The MTBR is 8458.92h for the Current policy, and 7113.54h for the Applied optimal policy. All this leads us to believe that there is much to be gained by optimization.

Next we compare the cost of the optimal Applied policy to that of the Theoretical one. If these two costs are similar, we may reasonably conclude that the proposed model will deliver similar performance. In the example, the cost of the applied policy is $0.195/h, and that of the theoretical one is $0.157/h. This difference is not very large (considering the sample size). From the theoretical policy, then, we would expect 97.74% preventive replacement, while only 92.31% = 12/13 would have been realized by applying the proposed policy retroactively. Similarly, from the theoretical projection, we expect the MTBR to be 7070.09h, but 7113.54h would have been realized in the sample. (For this sample size, these two values are very close, providing further confidence in the proposed model).

We now compare the results of the Fitted and Applied policies. Close cost values favor the conclusion that the optimal model is a good one. A significant difference in the costs may mean that some part of the theoretical model may be improved[22]. In the example, the cost of the fitted policy is $0.182/h, which is close to the cost $0.195/h of the applied policy. Both policies have one failed history, but different MTBRs - 7627h for the fitted policy, and 7113.54h for the applied. This means that the fitted policy would have performed better in selecting the moment for rework or discard[23].

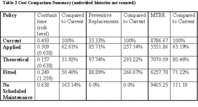
Table 3 provides the same type of information as Table 2 except that undecided histories are not counted. We include this additional analysis because it may be argued that we don't know how these histories will contribute to the average cost. If the proportion of undecided histories is not large, we may expect results in Table 3 to be similar to those of Table 2. Otherwise, we may expect the performance of the proposed model to lie somewhere between the boundaries defined by these two tables.

In summary

We evaluated a proposed optimal policy by considering its benefits in three ways: a) applied directly and retroactively to past data, b) fitted to past data, and c) fitted to expected cost. These analyses:

1. Provide ways to judge the potential benefits of a proposed CBM policy,
2. Use various sets of calculations to probe the economic robustness of the proposed CBM decision model, and
3. Are tools that a statistician or reliability engineer may use to gain a degree of comfort in the proposed policy’s future performance, by performing calculations at the edges of the “envelope” of possible solutions.

The assessment procedures described here provide, not only an objective way to assess actual (current) PM policy, but also ways to predict and evaluate the future cost advantages of proposed optimized policies.

Do you have any comments on this article? If so send them to murray@omdec.com.

[1] For some failure modes, where the failure progression can be read directly from the monitored variable, the measurement level at which a potential failure is declared may be reasonably based on human judgment and experience. The EXAKT methodology, however, recognizes the often probabilistic nature of a potential failure, and, therefore, defines a “best” decision (method of setting an action limit) that is based on a stated long-run optimizing objective.

[2] A software system developed at the University of Toronto for building and deploying CBM decision models as “intelligent agents”.

[3] Age exploration is a term that was used by Nowlan and Heap in their Reliability-centered Maintenance report of 1978 to describe any analytical process that considers an item’s past failure behavior in order to find ways to improve reliability and safety or to reduce cost.

[4] Observations, operating data, machinery signals, etc from which a potential failure may be deduced.

[5] A complex item is one that incurs two or more reasonably likely failure modes.

[6] “PM” in the general sense of proactive maintenance referring here to a policy of scheduled inspections (on-condition maintenance), scheduled rework, or scheduled discard.

[7] The EXAKT methodology is thoroughly examined in “Reliability-centered Knowledge” on page 178.

[8] Sample: Observations of an item’s (or group of similar items’) installations, failures, preventive renewals, significant events, and condition data over a period of time.

[9] Right suspensions. Equipment that is currently still operating at the time of the sample.

[10] We are considering two sets of calculations for the analyst to consider. It is a kind of best and worst case, with the actual situation being somewhere in the middle.

[11] Another calculation to help judge how well the EXAKT derived policy will do in the future

[12] “Undecided” means that it is unknown whether the item would have failed. The item was either still in operation or had been replaced preventively in the actual data set (sample)

[13] The optimal policy applied to the data would have permitted one failure to occur. That is the prediction method would have “missed” one time.

[14] The figure enclosed in parentheses in this table are the risk levels. The term “Risk level” denotes the product of failure probability and cost of the failure. It is included as a technical detail and does not enter into the assessment of the effectiveness of the proposed CBM policy.

[15] Still would have been functioning at the sample cut-off date.

[16] In Chapter 10. "Optimizing CBM" page 149 we perform a sensitivity analysis to determine how changes in the ratio will impact the optimal policy.

[17] The combined costs of all failures and all preventive repairs in the sample period.

[18] The analysis may also be done from the point of view of maximizing total availability, in which case costs would be replaced by “downtime” using the relationship Avail = uptime/ (uptime+downtime).

[19] 50.22% = 100% - 49.78%, 49.78% = 0.195/0.391

[20] (3+4)/13

[21] 12/13

[22] In this case we might re-investigate the state definitions we set up in the transition probability model. Ascertain that they are reasonable and no outliers are skewing the transition probabilities.

[23] One might ask, why not use the fitted policy then. Answer: the fitted policy can be obtained only after the fact. The purpose of evaluating a proposed policy in this way is to help judge its future effectiveness.

[24] The figure enclosed in parentheses in this table are the risk levels. The term “Risk level” denotes the product of failure probability and cost of the failure. It is included as a technical detail and does not enter into the assessment of the effectiveness of the proposed CBM policy.