Frequently asked questions
The following questions appeared recently
(July 2004) on the PlantMaint list service in response to the "Elusive P-F Curve" article that was
published at Reliabilityweb.com. http://www.reliabilityweb.com/art04/p-f_curve.htm
|
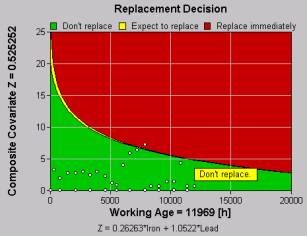
Question 1. Referring to your graph on the right, does EXAKT ignore “high points” that occur at a lower age and therefore do not cross over the green-to-red threshold? For example let’s say you have a sudden high vibration reading but it is still in the green region. Isn’t it dangerously negligent to ignore such a signal? |
|
Answer
Although EXAKT does not recommend a renewal for a
“high point” that is still in the green region, the
“abnormal” vibration reading may indeed be caused by problems (either not
directly related to the risk of failure or to the failure mode being addressed
by the model). For example, the item being monitored may be a complex item, one
that is subject to more than one failure mode. If that is the case, the
reliability engineer, may elect to build, and arm the EXAKT agent with, a second
decision model. The agent will sequentially apply the second model, one that
targets a (different) failure mode (whose risk of failure may be more
dominantly reflected by vibration[1]).
Alternatively, the reliability engineer may
manually add warning limits to the model to suggest, for example, a more
intrusive inspection of the unit, or a calibration check on the instrumentation
used in collecting the vibration data. In EXAKT, this feature sets up
descriptive warning limits that will be superimposed upon the optimal decision
graph. The warning limits act as additional guidance for maintenance personnel
to act[2].
A final point to note is that, the CBM Lab
designed EXAKT to extend current methods in on-condition maintenance.
Thus, if human interpretation of monitored data reveals a new failure mode, not
addressed by the current EXAKT model, the human expert may elect to update or
add this ‘new’ experience to the intelligent decision agent’s ‘knowledge base’.[3]
The “cost comparison” function in EXAKT provides a means for monitoring the
improving effectiveness (towards the attainment of an objective) of a
model as time proceeds and new
experience accrues.
The shape of the boundary curve in the
decision graph depends on the value of the shape parameter[4]
in the PHM (proportional hazards model). If the shape parameter equals 1, the
boundary curve will be a horizontal line. The graph shown above represents the
situation when the shape parameter is much greater than 1. In this instance,
the working age dominates the other significant risk factors, such as vibration
level, that you refer to in your question.
To explain this more clearly, we can treat
the age itself as a risk factor (the actual variable is log(age)) in the model.
Now we have two risk factors: the age and the vibration level. If
we fit the model[5] with shape
parameter fixed to one[6],
the model will be the same as one fitted with only a single risk factor, the
vibration level. (Of course, in the retained model, shape parameter is not
fixed to 1). The advantage of using a model that treats age as a risk factor is
that we can see the effect of age (compared with other factors) on the risk of
failure.
Using the actual EXAKT model, however,
we observe (by noting the shape of the boundary curve) that the shape
parameter is, in fact, greater than 1. That says that the risk of failure is
dominated by the age factor. It does not say that the vibration level is
not important. Instead, it says that the vibration level is not as
important as the age factor. Hence, in this instance, where a high vibration
level does appear at an early age, the decision graph in EXAKT advises that there is no need to renew[7]
the unit.
Question 2. SAE JA1011 states: “Any mathematical and statistical formulae that are used in the application of the [RCM] process (especially those used to compute the intervals of any tasks) shall be logically robust, and shall be available to and approved by the owner or user of the asset.” How does EXAKT meet this requirement?
Answer
As a general response, EXAKT’s algorithms’
statistical, mathematical, and logical robustness pass muster in the open
literature. Professional and academic
peer reviewed journals have published many papers that describe the CBM Lab’s
theoretical and practical development work in EXAKT. Here are just a few of those
references:
-
-
Jardine, A.K.S.,
Anderson, P. M. and Mann, D. S. (1987), “Application of the Weibull
proportional hazard model to aircraft and marine engine failure data”,
Quality & Reliability Engineering International, 5, 77-82.
- - Jardine, A.K.S., Banjevic, D., Wiseman, M., Buck S. and Joseph T. (2001). “Optimizing a mine haul truck wheel motor’s condition monitoring program: use of proportional hazards modeling”, Journal of Quality in Maintenance Engineering, Vol. 7, No. 4, pp. 286-301.
- - Makis, V. and Jardine, A.K.S. (1992). “Optimal replacement in the proportional hazards model”, INFOR, Vol. 30, pp.172-183.
-
- Vlok, P.J., Coetzee, J.L., Banjevic, D., Jardine, A.K.S. and Makis,
V. (2002), "Optimal Component Replacement Decisions using Vibration
Monitoring and the PHM", Journal of the Operational Research
Society, 53, pp. 193-202.
- - Daming Lin, Murray Wiseman, Dragan Banjevic, and A.K.S. Jardine (2004) "An approach to signal processing and condition-based maintenance for gearboxes subject to tooth failure" Mechanical Systems and Signal Processing, Volume 18, Issue 5 , September , Pages 993-1007
As a more specific answer we may discuss
some of the basic algorithms used in EXAKT. The first step in the development
of an EXAKT optimal decision model requires that we build a “proportional
hazard model”. The process consists of applying each variable monitored by a
CBM task to the EXAKT model creation process. In the procedure we test whether
a monitored variable does indeed correlate with past failures (functional or
potential). If it does, then that variable becomes a candidate for our
proportional hazard model. EXAKT uses an algorithm based on the Maximum
Likelihood Estimation method to fit the model to the available data. It then
uses extensive statistical testing to verify how good the resulting model
is.The figure below shows the window in EXAKT where these tests are initiated.

Once the
PHM is built and tested, we proceed to build the decision model. Once that is
done, we invoke additional statistical methods for investigating and testing
the decision model. A snapshot showing these features is shown below.
Finally,
once the reliability engineer is satisfied with the decision model, he (she)
exports it onto the network where it assumes the role of an “intelligent agent”
or “watchdog agent” that silently monitors new data as it arrives into one or
more databases[8]. The agent
generates its optimal interpretations as records in a database table. These
records may be accessed by the CMMS, ERP, or any other programs or humans
requiring the results of the CBM decision analysis.
Although
we have had several successful case studies with our industrial partners, the
final validation of the EXAKT methodology will be its wide acceptance and
implementation in industry. We are confident that this will come soon.
Question 3. Why at time zero does Z appear to be infinity?
Answer
The boundary curve corresponds to the
optimal hazard level h*. In other words, all the points on the curve have the
same hazard level h*. You can imagine doing a hazard rate contour plot here.
The boundary curve is the contour with hazard level h*. In this example
decision graph, the smaller the age, the bigger the value of Z should be to get
the same hazard level h*. This is why you observe a wider range of Z under the
boundary curve at earlier age. At age zero, any real value of Z will lead to a
zero hazard level. So, to have the same hazard level h* at age zero, Z must be
infinity. According to the way the decision graph is meant to be read, this
does not mean that you are going to have infinite Z in reality. The boundary
curve just divides the whole space for (age, Z) into two parts: the area under
the curve and the area above the curve. If the point (age0, Z0) corresponding
to your readings lies in the area above (under) the curve, it means that the
current hazard level is above (below) the optimal hazard level h* and the
decision would be to replace (not to replace) the unit. For more detail on the
decision graph, please see “Optimal replacement policy and the structure of
software for condition-based maintenance”, Journal of Quality in Maintenance,
V. 3, No. 2, pp109-119.