Why PHM? Incorporating Covariates in Weibull Analysis
By Naaman Gurvitz
Clockwork Solutions
Low
failure probabilities are critical factors in business
decisions when high costs are incurred due to the consequences of failure. In
these circumstances intensive data analysis efforts are employed to assess
probabilities of failure. Weibull analysis is commonly used to analyze data,
especially in cases where the propensity of failure increases with time and
use.
Data
analysis techniques and in particular Weibull analyses
are very sensitive to the 'mixing of populations', i.e. when operating
or environmental conditions that affect the failure rates, are totally ignored
or accounted for erroneously in the analysis. In general, the mixing of
populations in Weibull analysis will result in an underestimation of the shape
parameter. For example, consider three sets of 10 failure times, as listed in Table
1. When analyzing these data sets separately, we obtain three 'perfect'
Weibull fits, i.e. each set 'falls' exactly on a unique Weibull line as shown
in Figure 1 (with correlation coefficients ρ=1). It should be noted
that all three Weibull lines have the same shape parameter (slope) of β =
4.51. If all three sets are analyzed together as a single set, then the best
fit is a Weibull line with β = 2.46 (with ρ=0.95) as shown in Figure
2.
Table 1: Three sets of time observations
|
Group A |
Group B |
Group C |
|
26556 |
12645 |
9157 |
|
32729 |
15585 |
11286 |
|
36748 |
17499 |
12672 |
|
39989 |
19042 |
13789 |
|
42870 |
20414 |
14783 |
|
45605 |
21716 |
15726 |
|
48352 |
23025 |
16673 |
|
51298 |
24428 |
17689 |
|
54773 |
26082 |
18887 |
|
59847 |
28499 |
20637 |
In
summary, although the population size has increased three
times by analyzing the three sets together, the end result is (a) a
lower confidence in parameters estimates (i.e. a lower ρ) and (b) a
considerable underestimation of the shape parameter (β = 2.46 instead of
β = 4.51). The question is: are these consequences of mixing populations
important?
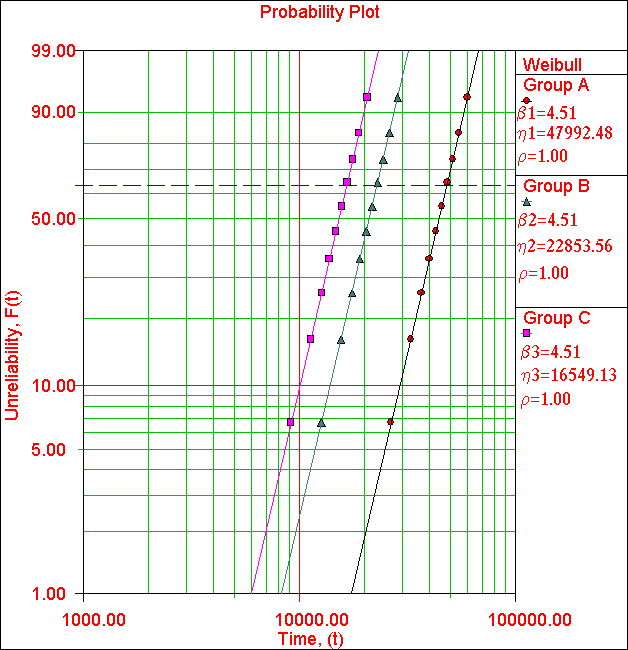
Figure 1: Weibull analysis of three individual sets
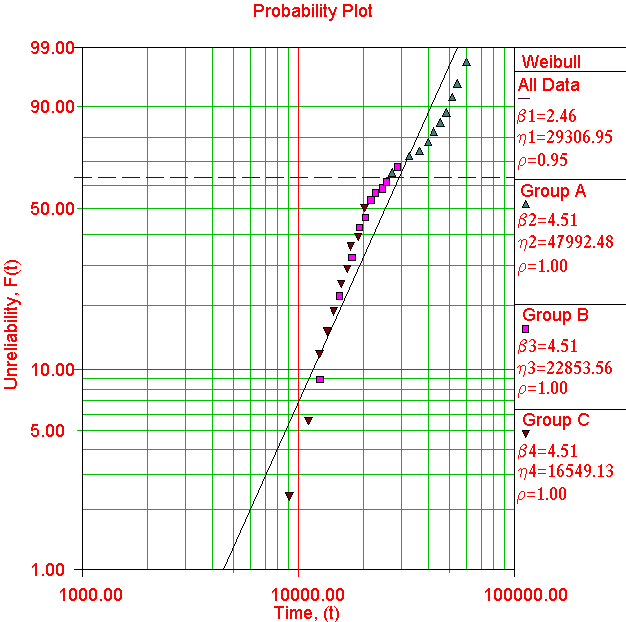
Figure 2: Weibull analysis with mixing populations
The
answer depends on the probability values of interest. But,
first it should be noted that Weibull distributions exhibit smaller variance
with increasing shape parameters. This phenomenon is especially noticeable in
the left-hand tail (or the head) of the Weibull distributions (i.e. for low
failure probabilities) as shown in Figures 3 and 4. Figure 3
displays cumulative probability functions CDF ([Note 1]) of Weibull distributions
with the same mean (mean = 48000 hours) but with different shape parameters
ranging from β=1 to β=10. Figure 4 focuses on the left-hand
side of the same Weibull distributions. So, if the probability values of
interest are approximately 50% (or around the mean) then there is no
significant difference between Weibull distributions with different shape
parameters (as
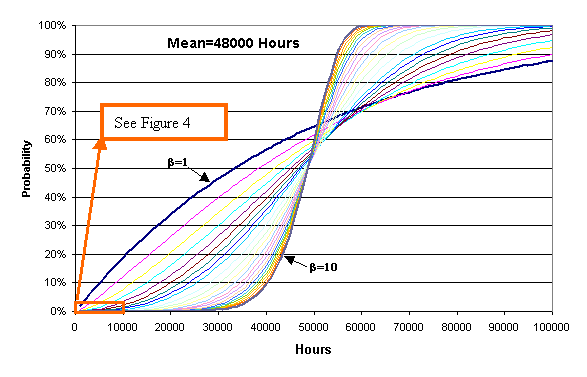
Figure 3: Failure probability curves for various
values of β
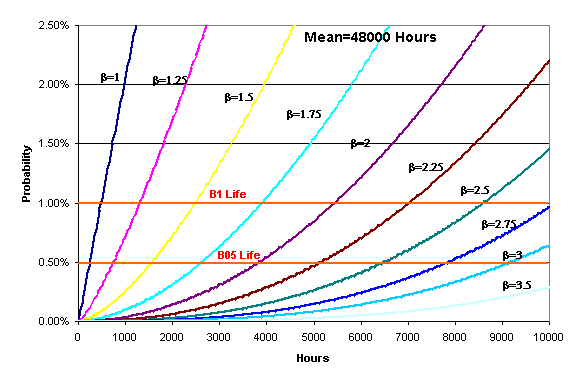
Figure 4: Failure probability curves at the lower
probability range of interst
in cases of sparing [Note 2] in which spares are used for replacement upon
failure), but if the focus is on low probability values of 5% or lower (as in
cases when preventive maintenance is employed to offset risk and overall cost
due to unscheduled failures) then differences in β values are very
significant.
Underestimation
of the shape parameter is equivalent to overestimation of the lower
ended probabilities. This overestimation is demonstrated by looking at B1 or B0.5 lives of components. BP life is defined as the time period
for which a new component will fail with a probability of P. (For example, the
B0.5 life is the time
period during which we are 99.5% confident that there will be no failure.) The
ratio between a BP life and
the mean [Note 3]
is independent of the scale parameter or the characteristic life (η) of
the distribution. Figure 5 shows a graph of B1 and B0.5 lives to mean ratios as a function of
β. Looking at the B1 life curve
we can conclude that an underestimation of β=4.51 value to β=2.46
will reduce the B1 time period
by approximately 23% of the mean (or a shortening of the time period by
approximately 58% compared to the 'actual' B1 period).
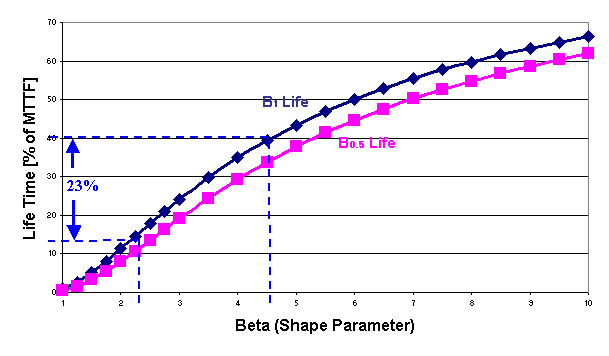
Figure 5: B1 and B0.5 lives to mean ratios as function of shape parameter
To
summarize, failure risk levels (expressed, for example,
as B1life) are less
sensitive to β at higher β values (Figure 4). The 'mixing of populations'
in Weibull analysis tends to underestimate β (Figure 2) and
consequently to underestimate B1 life (Figure 5). A robust data analysis methodology
that, in effect, 'separates' the entire population to statistically identical
subpopulations will result in more accurate and higher β values. This can
be accomplished by incorporating covariates in the Weibull analysis. By
covariates we mean any type of quantity that affects the failure rates and
can be attributed to every observation point, for example, type of fuel, number
of starts and so on. Unfortunately in reality covariates vary with time and
consequently each observation point is described by a whole 'history' of
varying covariate values. This situation is analogous to an attempt to separate
balls into groups according to their color while all the balls have many
stripes of different colors, and, therefore separation of populations prior to
Weibull analysis is simply an impossible task. However incorporating observed
covariates values into a Weibull Analysis such as Cox's Proportional Hazard
Model, that includes time-dependent covariates, overcomes this problem.
With such analysis techniques, a set of 'separated' Weibull curves (as in Figure
1) are obtained
[Note 4] rather than a single Weibull curve that includes the entire
population (as in Figure 2). This option is viable only if a whole
history of covariate values were indeed collected and this information can be
attributed to each of the observed time points. Today's data oriented
industrial and business environment favors such an extension of reliability
analysis.
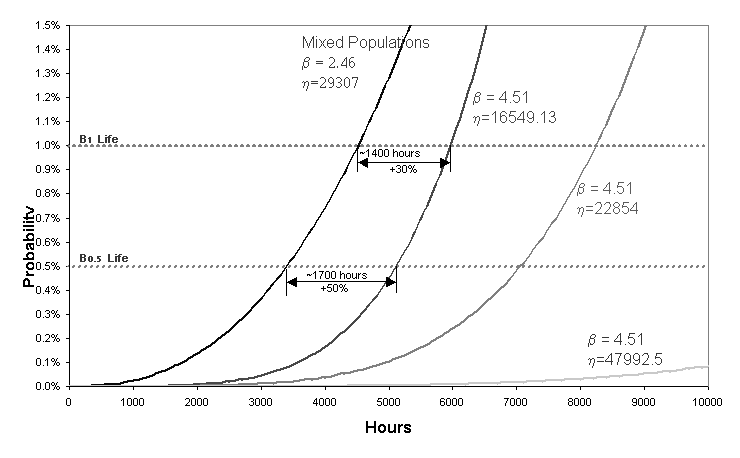
Figure 6: B1 and B0.5 lives (derived from Weibull analysis) with mixed and separated populations
Using the previous example, Figure 6 shows that the B1 and B0.5 life projections are, at minimum, 30%
and 50% respectively greater in a 'separated populations' analysis (resulting
in Weibull parameter estimates of η =16549 and β =4.51 for the worst
case), compared to projections from a 'mixed populations' analysis (resulting
in Weibull parameter estimates of η =29307 and β=2.46).
In
other words Weibull analysis has been thwarted by the indiscriminate mixing of these three populations whose
distinctive operating contexts have been unnaccounted for. This state of
affairs led us to underestimate the shape factor, which, in turn, caused us to
grossly underestimate the period of failure free operation. This weakness can
be overcome by including covariates that distinguish the operational
differences characterizing members of different populations. Furthermore,
monitored operating or sensor data, where available, can add even more veracity
to the predictive model. Naturally any additional data cleansing and analysis
is a time consuming effort, but this effort should be weighed against the
benefits of significant dollar savings through extended maintenance intervals.
Do you have any comments on
this article? If so send them to murray@omdec.com.
Notes:
1.
CDF, the cumulative distribution function is denoted by F(t) and
describes the probability of failure in a time period (ranging from 0 to time
t).
2.
It is assumed here, for purposes of illustration, that when
spares are available the probability of failure is quite high.
3.
Bp to Mean ratio:![]() where Γ is the Gamma function
where Γ is the Gamma function
4.
Actually what is obtained from analysis are estimates of Weibull
distribution parameters η, β and a set of covariates coefficients
γ1, γ2, …γn